タグ: 広大附属福山中学

明日は広大附属福山中学の試験日だ

 

 

 

積み重ねた時間、解いてきた問題、覚えたことすべてが、今日につながっている

 

 

 

広福の中学受験に挑む6年生は早く寝よう、そうしそう

 

 

 

暖めて、心も少しゆるめて寝よう

 

 

 

 

おやすみなさい

広大附属の受験生の内およそ半分くらいが岡山勢だから

 

 

 

 

 

合格者のうち60人ほどが岡山の小学生だと予想すると

 

 

 

 

 

岡山市や倉敷市の難関中学に進学する子が

 

 

 

 

 

 

10～20名ほど

 

 

 

 

 

また

 

 

 

 

 

広島市内や他県の難関中学に合格した子で

 

 

 

 

広大附属福山中を辞退する子たちが同じように10～20名ほどとする

 

 

 

 

 

すると

 

 

 

 

 

30名ほどは広大附属を辞退

 

 

 

 

 

もちろん年によって増減はある

 

 

 

 

 

広大附属福山は繰り上げ合格候補者から約30名を合格とするから

 

 

 

 

 

 

そのうち市立福山も受験していた生徒は15名、多くて20名ほど

 

 

 

 

やはり

 

 

 

 

結構な人数の子が繰り上げ合格になる

 

 

 

繰り上げ合格になるお子へ

 

 

 

 

 

中学入試の点差なんて大学入試の結果に一切影響しない

 

 

 

 

 

断言できる

 

 

 

 

 

 

だから

 

 

 

 

 

 

自信をもっていきたい中学校を選んでほしい

 

 

 

 

 

 

 

広大附属福山中学の入学手続きが締め切られる

 

 

 

 

 

明日以降

 

 

 

 

 

繰り上げ合格候補者の上位の順に、広大附属福山中学から連絡が入る

 

 

 

 

 

 

そうし広福の入学者が決まり

 

 

 

 

 

さらに

 

 

 

 

 

 

福山中学の繰り上げ合格の連絡が入っていく

 

 

 

 

 

 

 

市立福山の繰り上げ合格は広大附属福山の合格者に繋がっている

 

 

 

 

 

 

 

 

慶応義塾大学法学部合格おめでとう！

 

みんなの合格体験記を載せるのがのびのびになっているので。

 

去年ですが、もういい加減出さなきゃと思ってあわてて書いてます。よかったら是非！

 

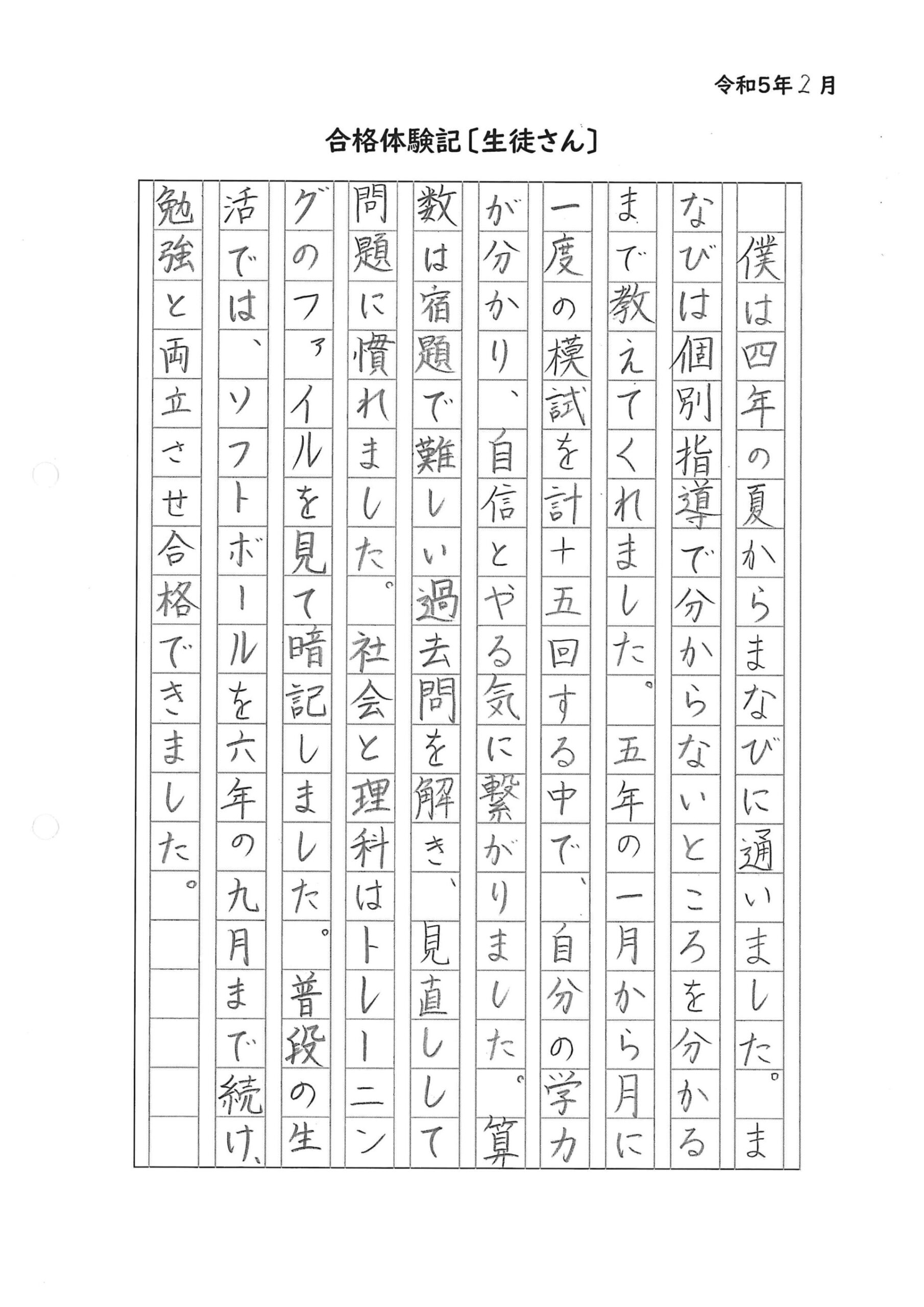
小学校4年生の時から通ってくれました。

 

国語は漢字博士な小学生でした。

 

塾まなびで中学受験をして広大附属福山中学校に合格、中2のときには全国作文コンクールでサクッと入選しました。

 

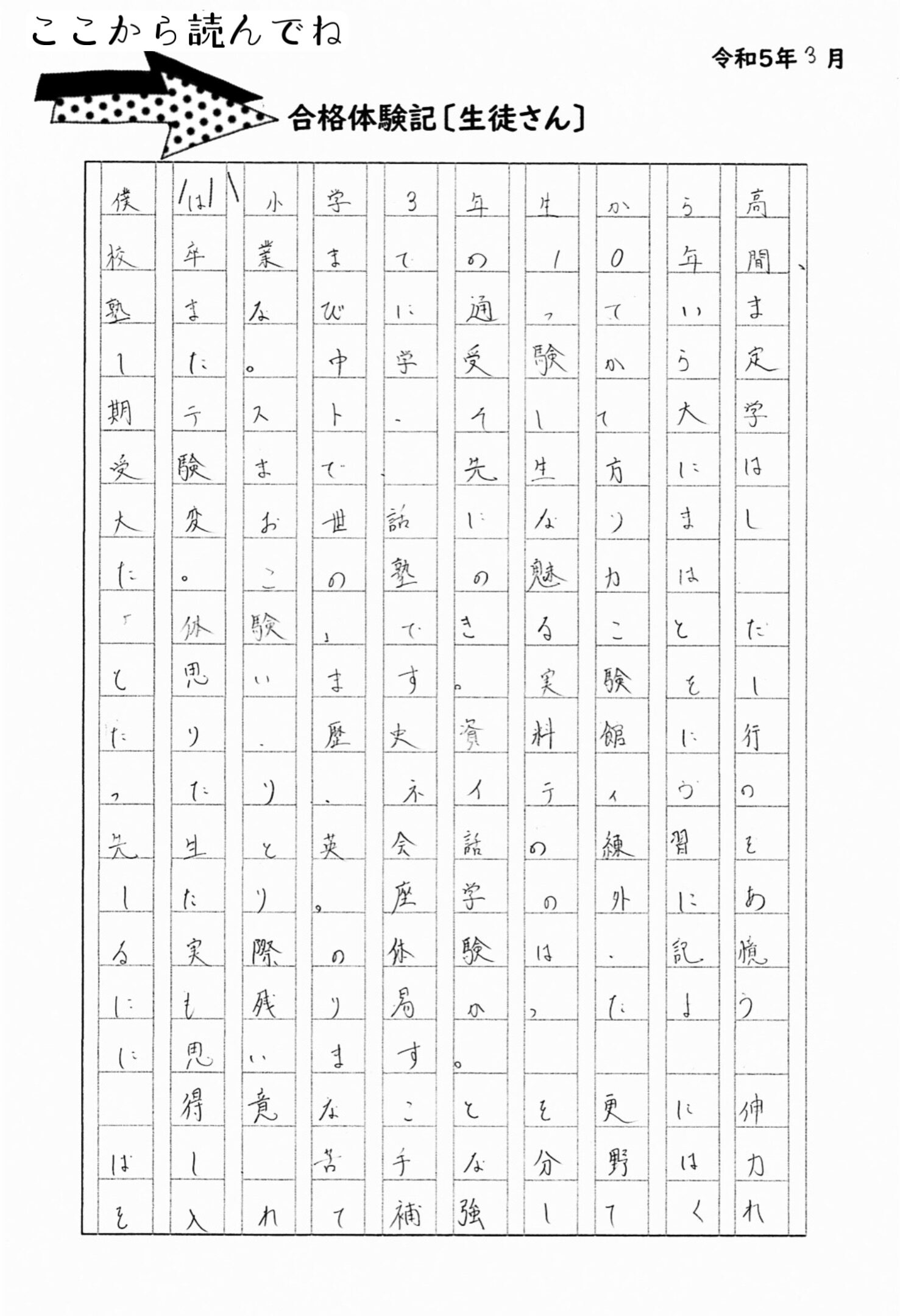
高校では広附で国語が学年トップになったこともありましたね。

 

英検準1級を高2のころに取得しています。

 

大学受験は一般入試で私学最難関の慶応義塾大学法学部に合格です。

 

国語で学年1位になったこともありましたね。もう大学合格はすっかり通り越して、もっと先を見据えてがんばっています。

 

合格体験記はコチラ

 

 

 

✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫
塾まなび（福山市にある個別指導塾）
確かな実力を身につける個別指導なら塾まなび
塾まなび本部　福山市明王台５丁目１７－２１
明王台校　　　福山市明王台３丁目２－２８
水呑校　　　　福山市水呑町三新田２－２９８ エーミック３３ ３号
代表　084-952-5845
info@juku-manabi.com
✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫

 

広大附属福山中学に合格です。おめでとう。中学受験したみんな、一人ひとり本当によくがんばりました。

 

この生徒も4年生のうちから塾まなびで広附をめざして努力していたので、一見すると着実に力をつけていったようにも見えます。

 

もしかしたら無難な受験、もともとすごく優等生で、できすぎ君なんじゃないって思う方もいらっしゃるかもしれません。

 

賢かったんでしょ、だからよねって、一直線に伸びていったイメージがするかもしれませんね。

 

いやね、でもそんなんじゃありません。

 

賢さはもちろんあるけど、すべてパーフェクトなはずはないんです。

 

そう、福山の公立小学校に通う、普通の小学生です。

 

やっぱりこう、学力は少しずつ上がり下がりがあったりしながら、全体としては伸びていく感じですね。

 

真っ直ぐ定規を引いた成長なんてないんですよね。

 

保護者の方の合格体験はコチラ

塾まなびの個別指導で国語もよくがんばったし、算数は難問もたくさん解けるようになった。

 

理科や社会は2学期以降、復習に時間をかけました。

 

入試までにはかなりの所まで仕上がっていました。

 

生徒の合格体験はコチラ

もちろん6年生になって大きく力を伸ばしたのは4年生、5年生からの塾でのがんばりが土台です。

 

受験期に悩みもあったし、中だるみだってそりゃあるよね。

 

でも丸ごとひっくるめて、保護者の方といっしょに本人のがんばりを教科や勉強に取り組むメンタル作りから全部、応援してきたからこその合格でした。

広大附属福山一択という中受でした。猛者ですね。

 

不必要なことは何もなかったよね。

よかったね、合格おめでとう。

 

広大附属福山中学合格って1番いい形で中学受験が終われました。

 

高いハードルを大きく越えたよね。

 

家中が合格したことに、まだふわふわした感じでいますって、お母さんやお兄さんが教えてくれました。

 

 

 

✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫

塾まなび（福山市にある個別指導塾）

確かな実力を身につける個別指導なら塾まなび

塾まなび本部　福山市明王台５丁目１７－２１

明王台校　　　福山市明王台３丁目２－２８

水呑校　　　　福山市水呑校４６５９－２　エーミック３３　３号

代表　０８４－９５２－５８４５

info@juku-manabi.com

✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫

このあいだの広大附属福山中学の算数と比べてみた件。

今回は東大2次〔2016年文系〕大問2です。

 

問題

A，B，C の3つのチームが参加する野球の大会を開催する。

以下の方式で試合を行い，2連勝したチームが出た時点で，

そのチームを優勝チームとして大会は終了する。

 

(a) 1試合目で A とB が対戦する。

 

(b) 2試合で，1試合目の勝者と，1試合目で待機していたCが対戦する。

 

(c) k試合目で優勝チームが決まらない場合は，k試合目の勝者と，

k試合目で待機していたチームがk+1試合目で対戦する。

 

ここでkは2以上の整数とする。

 

なお，すべての対戦において，それぞれのチームが勝つ確率は1/2で，

引き分けはないものとする。

 

(1)ちょうど5試合目でAが優勝する確率を求めよ。

 

1.対戦チームを書き出す。

 

2.規則性をみつける。

 

(ⅰ)1試合目でAが勝つとき，

 

 

(ⅱ)1試合目でBが勝つとき，

 

 

3.グループにする

 

このように書きだすと試合が無限に続く可能性もあることが分かりますね。

 

ではでは，このうち，

 

5試合目でAが優勝する可能性があるのは，

 

(ⅰ)のときだけで，

 

(ⅱ)では5試合目でAは試合をしていませんから無視すればいい。

 

よって，5試合目でAが優勝するパターンを書き出してみると，

 

 

 

(2)nを2以上の整数とする。ちょうどn試合目で A が優勝する確率を求めよ。

 

 

あとnが3の倍数のときも考えないとね。

 

3，6，9試合目ではAが優勝することはないから，

 

このときAが優勝する確率は0だけど，

 

ちゃんとすべてのnに対して答えを出すよ。

 

よって，

 

 

(3)mを正の整数とする。総試合数が3m回以下でAが優勝する確率を求めよ。

 

4.工夫して計算

 

最後はm乗にしてまとめました。

 

右の項を工夫して以下のように計算すると，まとめることができるよ。

 

1.数や文字を書き出す

2.規則性をみつける

3.グループにする

4.工夫して計算

 

こんなふうに本質的なところは同じだなぁと思う。

 

広大附属福山から東大と問題も繋がってる感がある気がします。

 

今日はこの辺で。

 

✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫

塾まなび

明王台校第１教室　広島県福山市明王台５丁目１７－２１

明王台校第２教室　広島県福山市明王台３丁目２－２８

水呑校三新田教室　広島県福山市水呑校４６５９－２　エーミック３３　３号

代表　０８４－９５２－５８４５

info@juku-manabi.com

✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫