このあいだの広大附属福山中学の算数と比べてみた件。
今回は東大2次〔2016年文系〕大問2です。
問題
A,B,C の3つのチームが参加する野球の大会を開催する。
以下の方式で試合を行い,2連勝したチームが出た時点で,
そのチームを優勝チームとして大会は終了する。
(a) 1試合目で A とB が対戦する。
(b) 2試合で,1試合目の勝者と,1試合目で待機していたCが対戦する。
(c) k試合目で優勝チームが決まらない場合は,k試合目の勝者と,
k試合目で待機していたチームがk+1試合目で対戦する。
ここでkは2以上の整数とする。
なお,すべての対戦において,それぞれのチームが勝つ確率は1/2で,
引き分けはないものとする。
(1)ちょうど5試合目でAが優勝する確率を求めよ。
1.対戦チームを書き出す。
2.規則性をみつける。
(ⅰ)1試合目でAが勝つとき,

(ⅱ)1試合目でBが勝つとき,

3.グループにする
このように書きだすと試合が無限に続く可能性もあることが分かりますね。
ではでは,このうち,
5試合目でAが優勝する可能性があるのは,
(ⅰ)のときだけで,
(ⅱ)では5試合目でAは試合をしていませんから無視すればいい。
よって,5試合目でAが優勝するパターンを書き出してみると,

(2)nを2以上の整数とする。ちょうどn試合目で A が優勝する確率を求めよ。

あとnが3の倍数のときも考えないとね。
3,6,9試合目ではAが優勝することはないから,
このときAが優勝する確率は0だけど,
ちゃんとすべてのnに対して答えを出すよ。
よって,

(3)mを正の整数とする。総試合数が3m回以下でAが優勝する確率を求めよ。

4.工夫して計算
最後はm乗にしてまとめました。
右の項を工夫して以下のように計算すると,まとめることができるよ。
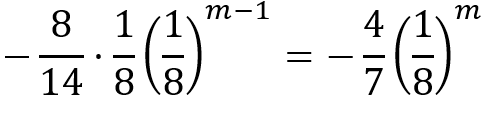
1.数や文字を書き出す
2.規則性をみつける
3.グループにする
4.工夫して計算
こんなふうに本質的なところは同じだなぁと思う。
広大附属福山から東大と問題も繋がってる感がある気がします。
今日はこの辺で。
✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫
塾まなび
明王台校第1教室 広島県福山市明王台5丁目17-21
明王台校第2教室 広島県福山市明王台3丁目2-28
水呑校三新田教室 広島県福山市水呑校4659-2 エーミック33 3号
代表 084-952-5845
info@juku-manabi.com
✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫✫